ドップラー効果

ドップラー効果の物理学。

ドップラー効果は、波の発生源と受信機がどのように動いているかによって波の周波数がどのように変化するかを記述します。ドップラー効果を説明するのに良く使われる例は、観測者を通り過ぎる救急車のサイレンの音です。救急車の動きにより、救急車の前方に発出される音波が圧縮され、後方に発出される音波は引き伸ばされます。観測者はこの効果をサイレンのピッチの変化として認識します。救急車が観測者に向かって進む間は音程は高くなります。救急車が離れ始めるとすぐに音程が低くなります。

音波の周波数変化は、音源と受信者の相対移動速度に依存します。1842年の出版物「連星や他の星の光の色について」で、ドップラーは観測者が測定する周波数を計算する次の公式を提示しました。

この式は
   、観測者が測定する周波数
   発信源が発出する周波数
   観測者の運動速度
  発信源の運動速度
  媒体中の波の伝搬速度（波速）が

状況 1:受信機が静止し、発信源が動いている場合:

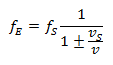
状況 2:発信源が静止し、受信機は動いている場合:

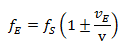
この２つの式がドップラー効果を記述しています。周波数の変化は発信源と観測者が音波の伝搬媒体に対して運動している速度に依存します。これはドップラーの時代における偉大な発見でした。ドップラーはその著作の中で、「光の色と周波数の変化は主観的なものではなく、客観的な事実である」と述べています。

光とドップラー効果

クリスティアン・ドップラーは、この効果は音以外の全てのタイプの波についても有効なはずであると推定しました。当時の科学では、光は「エーテル」と名づけられた未知の伝搬媒質中を伝わるという理解でした。アルバート・マイケルソンとエドワード・モーレイが、マイケルソン‐モーレイの実験で、光の伝搬を担うそのような「エーテル」は存在しないことを証明したのは、1881年と1887年の研究成果でした。今日、古典的ドップラー効果は、媒質中を伝搬する波に対する現象にのみ適用されています。

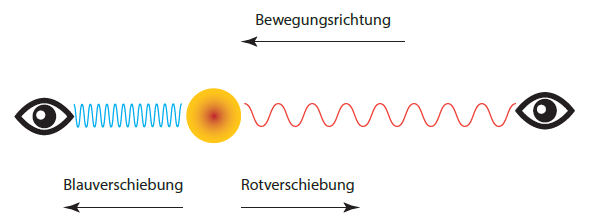
しかし、伝搬物質無しでも、電磁波にドップラー効果が働くことが、わかっています。光源が観測者に向かい運動しているときには、光の波長が圧縮されて青色に偏移し、光源が観測者から遠ざかる運動をしているときには、光の波長が引き延ばされて赤色に偏移します（図参照）。

電磁波においては、ドップラー効果は発信源と伝送媒体の相対速度ではなく、発信源と受信者の相対速度に依存します。受信周波数 と送信周波数 は次の式で関係づけられます:

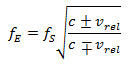
このドップラー効果の公式では、 c は 299 792 km/sの光速を、 は光源と受信者の相対速度を表します。

ドップラー公式の実際の応用例

以下に、音波が空中を伝搬する二つの事例を示します。

事例１: 受信機が静止していて、音源が受信機に向かっている (-) あるいは遠ざかっている (+)場合。

ドップラー公式では、

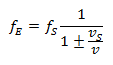
例えば、音源となる車が時速 130 km/h (秒速約 36 m/s) で、道端に立っている受信者となる歩行者のそばを通過する場合を考えましょう。運転者と歩行者は知り合いで、運転者が歩行者にクラクションを鳴らして合図します。クラクションの周波数は 1000 ヘルツです。では歩行者に聞こえるクラクションの周波数は、いくらになるでしょう。

車が近づくとき、歩行者に聴こえる周波数は、

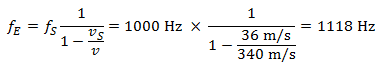
車が遠ざかるとき、周波数は 904Hzにまで下がります。

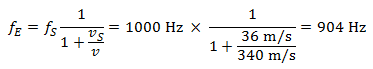
こうして、車が接近するとき、周波数は 118 ヘルツ増加し、車が遠ざかるときは 96 ヘルツ減少します。 1000 ヘルツの音は音楽の五線譜で二線上の高い「ド」の音に対応します。この例での音程変化は小さく、半音階の上下に相当します。

事例２: 音源が静止していて受信機が音源に近づく (+) か、遠ざかる (-)場合。

ドップラー公式は、

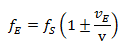
次の例ではで、時速 130 km/h (秒速約 36 m/s)で疾走する車の運転手が受信者で、知り合いの歩行者が、運転手に周波数1000ヘルツの警笛を鳴らして挨拶する場合を考えましょう。

歩行者に近づくとき、運転手に聴こえる周波数は

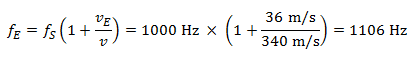
歩行者から遠ざかるとき、運転手に聴こえる周波数は

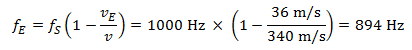
この場合、運転手が聴く音の周波数変化は上下とも 106 ヘルツとなります。/p>

これら二つの場合で周波数変化が異なるのは、音の伝搬媒質となる空気との相対速度が関係するからです。第一の場合では音源が動くのに対し、第二の場合では受信者が動くところが違っています。

Based on the book:

Christian Doppler – Der für die Menschheit bedeutendste Salzburger, Clemens M. Hutter, Verlag Anton Pustet 2017

Further information on the Doppler effect | hyperphysics.phy-astr.gsu.edu